71 图的定义与操作
图的定义与操作
-
讨论中......
A:树中的结点可以有多个后继,而每个结点都只有一个直接前驱,因此形成了一种层次结构。 B:如果树中的每个结点也可以有多个直接前驱,那么这种层次结构都被破坏了。 C:这样子就形成了网状结构,会是一种新的数据结构么?
-
定义 图是由顶点集合(Vertex)及顶点间的关系集合(Edge)组成的一种数据结构: Graph=(V,E)
V={x|x∈某个数据对象}是顶点的有穷非空集合E={(x,y)|x,y∈V}是顶点之间关系的有穷集合 -
问题 思考:G1,G2,G3,G4都有图么?有什么异同?可以继续分类吗?
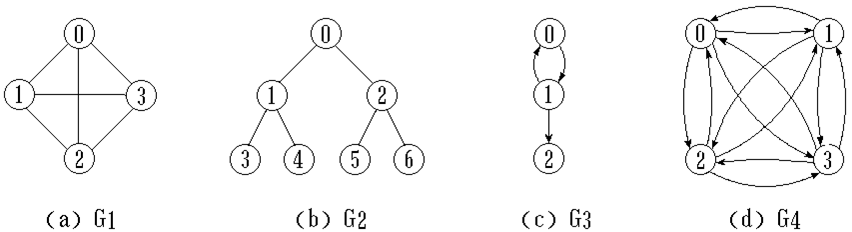
-
无向边
- 顶点x和y之间的边没有方向,则称该边为无向边
- (x,y)与(y,x)意义相同,表示x和y之间有连接
-
无向图
- 图中任意两个顶点之间的边均是无向边,则称该图为无向图
-
有向边
- 顶点x和y之间的边有方向,则称该边为有向边
<x,y>与<y,x>意义不同<x,y>表示从x连接到y,x称为尾,y称为头<y,x>表示从y连接到x,y称为尾,x称为头
-
有向图
- 图中任意两个顶点之间的边均是有向边,则称该图为有向图
-
有向图示例
无向图可以看作一种特殊的有向图!
-
顶点邻接(Adjacent)的定义
- 无向图
- 如果(x,y)∈E,则称顶点x和y互为邻接
- 有向图
- 如果< x,y >∈E,则称顶点x邻接到顶点y
- 无向图
-
度(Degree)的定义
- 顶点v的度是和v相关联的边的数目,记为TD(v)
- 入度:以v为头的边的数目,记为ID(v)
- 出度:以v为尾的边的数目,记为OD(v)
- 顶点v的度是和v相关联的边的数目,记为TD(v)
-
推论
- TD(v)=ID(v)+OD(V)
- Count(E)=ID(v1)+ID(v2)+...+ID(vn)
- Count(E)=OD(v1)+OD(v2)+...+OD(vn)
- Count(E)=[TD(v1)+TD(v2)+..+TD(vn)]/2
-
权(Weight)的定义
- 与图的边相关的数据元素叫做权
- 权常用来表示图中顶点间的距离或者耗费
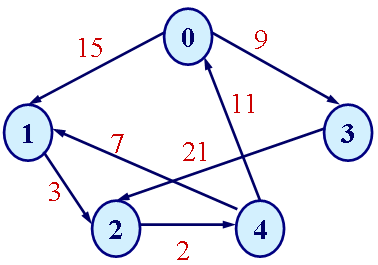
-
图的一些常用的操作
- 设置顶点的值
- 获取顶点的值
- 获取邻接顶点
- 设置边的值
- 删除边
- 获取顶点树
- 获取边树
- ......
-
图在程序中表现为一种特殊的数据类型
templat<typename VertexType,typename EdgeType>
class Grap:public Object{
public:
virtual VertexType vertex(size_t index)=0;
virtual bool vertex(size_t index,VertexType &value)=0;
virtual bool setVertex(size_t index,const VertexType &value)=0;
virtual SharedPointer<Array<size_t>> adjacent(size_t index)=0;
virtual EdgeType egde(size_t begin,size_t end)=0;
virtual bool egde(size_t begin,size_t end,EdgeType &value)=0;
virtual bool setEdge(size_t begin,size_t end,cosnt EdgeType &value)=0;
virtual bool removeEdge(size_t begin,size_t end)=0;
virtual size_t vertexCount()=0;
virtual size_t edgeCount()=0;
virtual size_t outDegree(size_t index)=0;
virtual size_t inDegree(size_t index)=0;
virtual size_t degree(size_t index) {
return outDegree(index)+inDegree(index);
}
}
编程实验
-
图抽象类的创建
小结
- 图是顶点与边的集合,是一种非线性的数据结构
- 图中顶点可以与多个其它顶点 产生邻接关系
- 图中的边有与之对应的权值,表示顶点间的距离
- 图在程序中表现为特殊的数据类型
72 图的存储结构(上)
图的存储结构(上)
-
基本思想
- 用一维数组存储顶点:描述顶点相关的数据
- 用二维数组存储边:描述顶点间的关系和权
-
邻接矩阵法
-
设图A=(V,E)是一个有n个顶点的图。图的邻接矩阵为Edge[n][n],则:
注:解决工程问题时,习惯于对图中的每个顶点进行编号;当不需要权值时,取W非空表示结点间有连接。
-
-
邻接矩阵法示例一
-
无向图的邻接矩阵是对称的
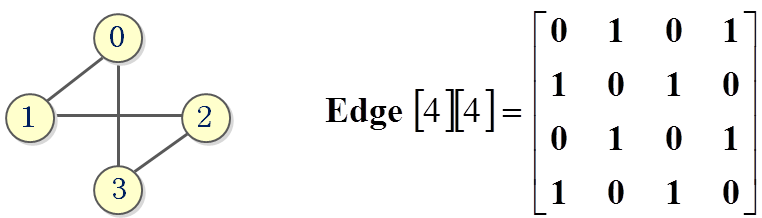
-
-
邻接矩阵法示例二
-
有向图的邻接矩阵可能是不对称的
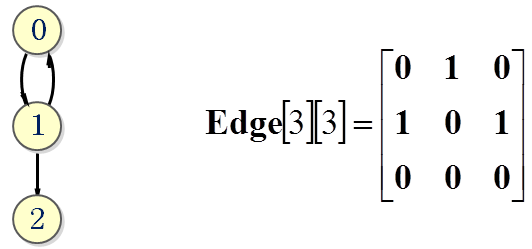
-
-
设计与实现
问题:如何具体表示顶点集数组?如何具体表示边集数组?
-
实现方式一:直接使用数组表示顶点集和边集
template<int N,typename VertexType,typename EdgeType>
class MatrixGraph:public Graph<VertexType,EdgeType>{
protected:
VertexType m_vertexes[N];
EdgeType m_edges[N][N];
int m_eCount;
public:
//...
} -
分析下面代码的效率
struct TV{
int a1[100];
char a2[1000];
TV(){/*init array*/}
};
struct TE{
float a1[100];
float a2[1000];
TE(){/*init array*/}
};
int main(){
MatrixGraph<1000,TV,TE> g;
} -
问题
- 构造效率低下
- 图对象初始化时,频繁调用顶点类型和边类型的构造函数
- 空间使用率低下
- 图对象占用大量空间,而大多数空间处于闲置状态
- 无法表示空值
- 无法用统一的方式表示边为空的情形
- 构造效率低下
-
实现方式二:使用指针数组表示顶点集和边集
template<int N,typename VertexType,typename EdgeType>
class MatrixGraph:public Graph<VertexType,EdgeType>{
protected:
VertexType *m_vertexes[N];
EdgeType *m_edges[N][N];
int m_eCount;
public:
//...
} -
问题的解决
- 构造效率
- 初始化图像时,只需要将数组元素赋值为空
- 空间使用率
- 顶点数据元素和边数据元素在需要时动态创建
- 空值的表示
- 任意的顶点类型和边类型都使用nullptr空值表示
- 构造效率
编程实验
-
图的邻接矩阵结构
小结
- 邻接矩阵法使用数组对图相关的数据进行存储
- 一维数组存储顶点相关的数据(空表示无相关的数据)
- 二维数组存储边相关的数据(空表示顶点间无连接)
- 代码实现时,使用指针数组进行数据的存储(提高效率)
73 图的存储结构(下)
图的存储结构(下)
-
邻接矩阵法中的残留问题 MatrixGraph无法动态添加/删除顶点!
template<int N,typename V,typename E>
class MatrixGraph:public Graph<V,E>{
public:
//......
protected:
V *m_vertexes[N];
E *m_edges[N][N];
int m_eCount;
};
/*N=1000,邻接矩阵的体积为4*1000*1000字节;因此,图对象创建时的体积约为4MB!*/ -
基本思想 为了进一步提高空间使用率,可以考虑使用链表替换数组,将邻接矩阵变换为邻接链表......
-
邻接链表法
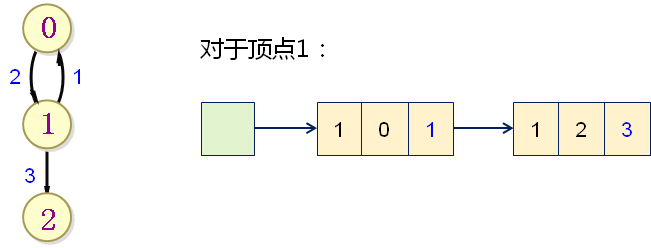
- 图中的所有顶点按照编号存储于同一个链表中
- 每一个顶点对应一个链表,用于存储始发于该顶点的边
- 每一条边的信息包含:起点,终点,权值
-
邻接链表法示例
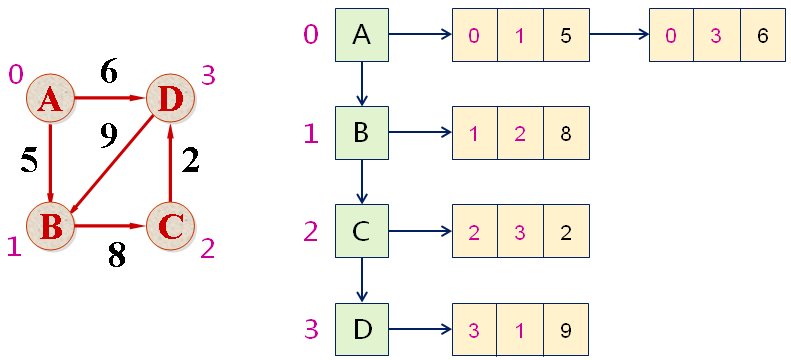
-
设计与实现
-
边数据类型的设计
struct Edge:public Object{
int b; //起始顶点
int e; //邻接顶点
E data; //权值
//...
}; -
顶点数据类型的设计
struct Vertex : public Object{
V *data; //顶点数据元素值
LinkList<Edge> edge;//邻接于该顶点的边
//...
}; -
动态增加/删除顶点
int addVertex();- 增加新的顶点,返回顶点编号
int addVertex(const V &value);- 增加新顶点的同时附加数据元素
void removeVertex()- 删除最近增加的顶点
编程实验
-
图的邻接链表结构
小结
- 邻接链表法使用链表对图相关的数据进行存储
- 每一个顶点关联一个链表,用于存储边相关的数据
- 所有顶点按照编号被组织在同一个链表中
- 邻接链表法实现的图能够支持动态添加/删除顶点